Refraction

A ball is pushed from A to B.

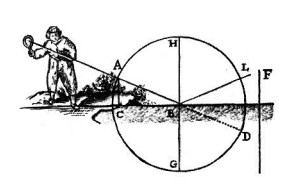
It encounters at B not the surface of the Earth, but a thin and delicate fabric CBE. It is so weak that the ball can break through and pass through it, only losing half its speed.

What path will it take?

Its motion differs entirely from its determination to move towards one side rather than the other.

Therefore, their quantities must be examined separately.

Two force make up the movement of the ball:

• The horizontal
• The vertical

Of these two, only the vertical force can be altered by the encounter with the fabric.

The vertical force remains unchanged because the fabric does not oppose it in that direction.

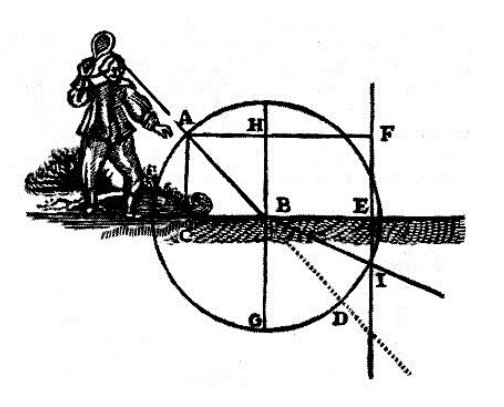
Circle AFD has its center at B. It has 3 straight lines AC, HB, FE perpendicular to CBE.

• The distance between AC and HB is half as that between HB and FE.

We will see that the ball must tend towards point I.

This is because it loses half its speed in crossing the canvas CBE. And so it must take twice as long to pass below, from B to some point on the circumference of the circle AFD, as it took it to come from A to B above.

• It does not change its rightward motion.

And so in twice the time it took to pass from the line AC to HB, it must make twice as much progress towards that same side.

Consequently, it would arrive at some point on the straight line FE, at the same instant that it also arrives at some point on the circumference of the circle AFD.

It must go to I since that is the only point below the canvas CBE where the circle AFD and the straight line FE intersect.

Let us now imagine that the ball, coming from A towards D, meets at point B water. Its surface CBE takes away exactly half of its speed, just as that canvas did.

This ball must pass from B in a straight line, towards I.

This is because the water’s surface must turn it towards there in the same way as the canvas, since it takes away just as much of its force, and is opposed to it in the same direction.

The rest of the water that fills the space from B to I resists it more than the air.

Since it loses half of its velocity while crossing the fabric CBE, it must take twice as much time to pass below from B to some point on the circumference of the circle AFD as it took to come from A to B above.

It does not lose any of the determination. And so it must:

• advance towards the right side, in twice the amount of time it took to pass from line AC to HB
• cover twice the distance towards the same side

Consequently, it would reach some point on the straight line FE when it also reaches some point on the circumference of the circle AFD.

This would be impossible if it did not go towards I, given that it is the only point below the fabric CBE where the circle AFD and the straight line FF intersect.

The ball is deflected all the more by the surface of the water or the net, the more obliquely it encounters it.

If it encounters it at a right angle, as when it is pushed from H to B, it must pass straight through in a line towards G, without deviating at all.

But if it is pushed along a line like AB, which is so inclined with respect to the surface of the water or the net CBE, that the line FE, being drawn as before, does not cut across the circle AD, this ball would not penetrate it at all.

Instead, it would bounce back from its surface B into the air L, just as if it had encountered earth.

This actually happened when artillery was fired towards the bottom of a river for entertainment.

• Those on the opposite bank were injured.