Reflection

How can we determine this refraction quantitatively?

To answer this, we must first explain reflection.

Suppose a ball is struck from A towards B. At B it meets the surface of the ground CBE, which prevents it from going further and causes it to be deflected.

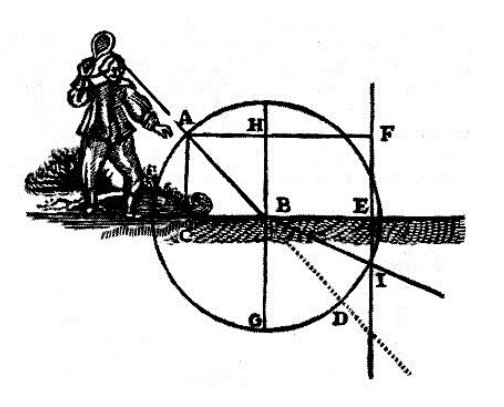
• The ground is perfectly flat and hard.
• The ball always travels at a constant speed, both when it descends and rebounds upwards.

Where will it go?

The Directional Force

The force that causes the speed of the ball is different from the force that causes the direction of the ball. That direction is determined by the position of the racket.

This directional force shows that this ball can be diverted by the encounter with the earth CBE.

Thus, CBE can change the direction that it had towards B without changing the force that gave its speed, since these are 2 different things.

This is why it does not have to stop at B before bouncing off to F as many of our Philosophers think. If it was stopped at B then there is nothing at B which can cause it to start again.

The determination to move towards a certain side, as well as movement and generally any other kind of quantity, can be divided between all the parts that compose it.

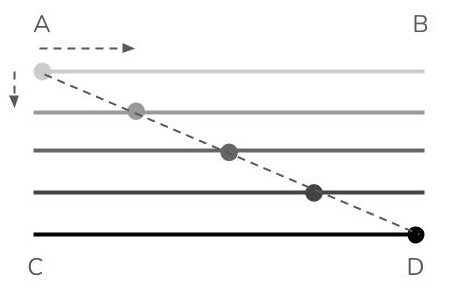
A ball that moves from A to D is composed of 2 others:

1. A force which makes it fall from the line AB to the line CD
2. A force which makes it go from the left AC to the right BD

These together lead it to D along the straight line AD.

The encounter with the earth can only prevent one of these two determinations, and not the other.

• It prevents the one that made the ball fall from AB to CD because it occupies all the space that is below CD.

Let us draw a circle with center B, which passes through line A which is the path of the ball.

The ball would have travelled from in the same time from B to some point on the circle’s circumference, as it travelled from A to B.

This is because we suppose that:

• all the points in the circle are as distant from B as A is.
• the ball’s speed is always equally fast.*

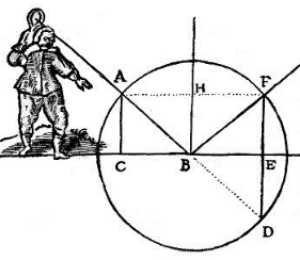
To know where on this circle the ball must end up, let us draw 3 straight lines AC, HB, FE perpendicular to CE.

• The distance between AC and HB is the same as that between HB and FE.

Assume that it will take the ball travelling rightwards the same time to go from point A to point B and from B to any point in the circle that touches line FE. In this case, it is F or D.

Thus, if the Earth prevents it from passing towards D, then it must go towards F.

This is how reflection occurs at an angle always equal to what is called the angle of incidence.

For example, if a ray coming from point A falls on point B on the flat mirror CBE, it reflects towards F in such a way that the angle of reflection FBE is neither greater nor smaller than the angle of incidence ABC.