Proposition 53, Theorem 41

Bodies carried around in a vortex, and returning in the same orb, are of the same density with the vortex.

They are moved according to the same law with the parts of the vortex, as to velocity and direction of motion.

The particles or physical points of the vortex preserve a given situation among each other.

If these particles are be congealed, this particle will move according to the same law as before. This is because no change is made either in its density, vis insita, or shape.

This fluid vortex will move according to the same law as before if its congealed or solid part is of the same density with the rest of the vortex.

• Its fluid particles may be moved among themselves.

Neglect the motion of the particles among themselves.

• This is because it does not concern at all the progressive motion of the whole.
• This will lead to the motion of the whole being the same as before.

But this motion will be the same with the motion of other parts of the vortex at equal distances from the centre.

• This is because the solid, now resolved into a fluid, is become perfectly like to the other parts of the vortex.

Therefore a solid, if it be of the same density with the matter of the vortex, will move with the same motion as its parts, being relatively at rest in the matter that surrounds it.

If it is more dense, it will try more to move away from the centre.

It will overcome that force of the vortex which is kept in equilibrio while it was retained in its orbit.

It will move away from the centre and will follow a spiral, leaving its orbit.

If it be more rare, it will move to the centre.

Therefore it can never continually go around in the same orbit unless it is of the same density with the fluid.

But in that case, it would revolve according to the same law with those parts of the fluid that are at the same or equal distances from the centre of the vortex.

Corollary 1

Therefore a solid revolving in a vortex, and continually going round in the same orbit, is relatively quiescent in the fluid that carries it.

Corollary 2

If the vortex has a uniform density, the same body may revolve at any distance from the vortex’ centre.

SCHOLIUM

Hence, the planets are not carried round in corporeal vortices.

According to the Copernican hypothesis, the planets going round the sun revolve in ellipses. They have the sun in their common focus.

The radii drawn to the sun draw areas proportional to the times.

But the parts of a vortex can never revolve with such a motion.

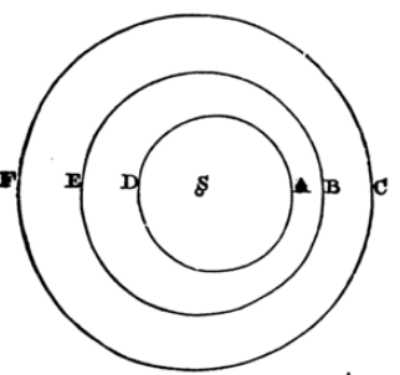
Let AD, BE, CF be 3 orbits around sun S.

• The utmost circle CF is concentric to the Sun

The aphelia of the two innermost are A, B. Their perihelia D, E.

Therefore a body revolving in the orb CF, draws by a radius drawn to the sun, areas proportional to the times. These will move with an uniform motion.

According to the laws of astronomy, the body revolving in the orb BE will move:

• slower in its aphelion B
• faster in its perihelion E

According to the laws of mechanics, the matter of the vortex should move faster in the narrow space between A and C than in the wide space between D and P.

• It should faster in the aphelion than in the perihelion.

These 2 conclusions contradict each other.

The aphelion of Mars is currently at the beginning of Virgo.

The distance between the orbits of Mars and Venus now is around 3 to 2 their distance at the beginning of Pisces.

Therefore, the vortex matter between those orbits should faster at the beginning of Pisces than at the beginning of Virgo in the ratio of 3 to 2.

This is because the narrower the space is through which the same quantity of matter passes in the same time of one revolution, the greater will be the velocity with which it passes through it.

[Descartes assumes] that the earth:

• is relatively at rest in this celestial matter
• is carried around by it
• revolves together with it around the sun.

If so, the earth’s velocity at the beginning of Pisces would be have a sesquialteral ratio to its velocity at the beginning of Virgo.

Therefore, the sun’s apparent diurnal motion:

• at the beginning of Virgo should be above 70 minutes
• at the beginning of Pisces shuld be less than 48 minutes

But in reality, that apparent motion of the sun is really greater at the beginning of Pisces than at the beginning of Virgo.

Therefore the earth is faster at the beginning of Virgo than at the beginning of Pisces.

Thus, the hypothesis of vortices is utterly irreconcileable with astronomical phenomena. It rather perplexes than explains the heavenly motions.

Book 1 explains how these motions are performed in free spaces without vortices.