Scholium: Newton's Cradle

Thus, trying the thing with pendulums of 10 feet, in unequal as well as equal bodies, and making the bodies to concur after a descent through large spaces, as of 8, 12, or 16 feet,

I found always, without an error of 3 inches, that when the bodies concurred together directly, equal changes towards the contrary parts were produced in their motions,

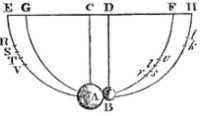
consequence, that the action and reaction were always equal.

Body A impinged on body B at rest with 9 parts of motion, and losing 7.

It then proceeded after reflexion with 2.

Body B was carried backwards with those 7 parts.

If the bodies concurred with contrary motions, A with 12 parts of motion, and B with 6, then if A receded with 2, B receded with 8 to wit, with a deduction of 14 parts of motion on each side.

For from the motion of A subducting 12 parts, nothing will remain.

But subducting 2 parts more, a motion will be generated of 2 parts towards the contrary way.

And so, from the motion of the body B of 6 parts, subducting 14 parts, a motion is generated of 8 parts towards the contrary way.

But if the bodies were made both to move towards the same way, A, the swifter, with 14 parts of motion, B, the slower, with 5, and after reflexion A went on with 5, B likewise went on with 14 parts; 9 parts being transferred from A to B.

And so in other cases.

By the congress and collision of bodies, the quantity of motion, collected from the sum of the motions directed towards the same way, or from the difference of those that were directed towards contrary ways, was never changed.

For the error of an inch or two in measures may be easily ascribed to the difficulty of executing everything with accuracy.

It was not easy to let go the two pendulums so exactly together that the bodies should impinge one upon the other in the lowermost place AB; nor to mark the places s, and k, to which the bodies ascended after congress.

Some errors, too, might have happened from the unequal density of the parts of the pendulous bodies themselves, and from the irregularity of the texture proceeding from other causes.

But to prevent an objection that may perhaps be alledged against the rule, for the proof of which this experiment was made, as if this rule did suppose that the bodies were either absolutely hard, or at least perfectly elastic (whereas no such bodies are to be found in nature), I must add, that the experiments we have been describing, by no means depending upon that quality of hardness, do succeed as well in soft as in hard bodies.

For if the rule is to be tried in bodies not perfectly hard, we are only to diminish the reflexion in such a certain proportion as the quantity of the elastic force requires.

By the theory of Wren and Huygens, bodies absolutely hard return one from another with the same velocity with which they meet.

But this may be affirmed with more certainty of bodies perfectly elastic. In bodies imperfectly elastic the velocity of the return is to be diminished together with the elastic force; because that force (except when the parts of bodies are bruised by their congress, or suffer some such extension as happens under the strokes of a hammer) is (as far as I can perceive) certain and determined, and makes the bodies to return one from the other with a relative velocity, which is in a given ratio to that relative velocity with which they met. This I tried in balls of wool, made up tightly, and strongly compressed.

For, first, by letting go the pendulous bodies, and measuring their reflexion, I determined the quantity of their elastic force; and then, according to this force, estimated the reflexions that ought to happen in other cases of congress.

With this computation other experiments made afterwards did accordingly agree; the balls always receding one from the other with a relative velocity, which was to the relative velocity with which they met as about 5 to 9.

Balls of steel returned with almost the same velocity: those of cork with a velocity something less; but in balls of glass the proportion was as about 15 to 16. And thus the third Law, so far as it regards percussions and reflexions, is proved by a theory exactly agreeing with experience.