Illustrations

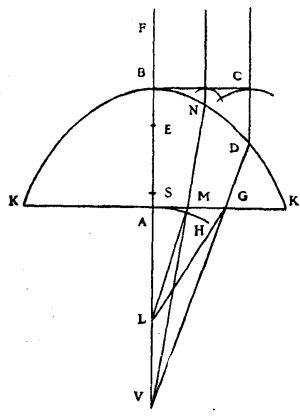
To demonstrate the effect of the curve, let there be:

• a circular arc AH around the centre L, cutting LG at H.
• around the centre F the arc BP
• in AB let AS be equal to 2/3 of HG and SE equal to GD.

Then considering AH as a wave of light emanating from the point L, it is certain that during the time in which its piece H arrives at G the piece A will have advanced within the transparent body only along AS; for I suppose, as above, the proportion of the refraction to be as 3 to 2.

The piece of wave which is incident on G, advances thence along the line GD, since GV is the refraction of the ray LG.

Then during the time that this piece of wave has taken from G to D, the other piece which was at S has reached E, since GD, SE are equal.

But while the latter will advance from E to B, the piece of wave which was at D will have spread into the air its partial wave, the semi-diameter of which, DC (supposing this wave to cut the line DF at C), will be 3/2 of EB, since the velocity of light outside the medium is to that inside as 3 to 2.

This wave will touch the arc BP at C.

For since, by construction, FD + 3/2 DG + GL are equal to FB + 3/2 BA + AL; on deducting the equals LH, LA, there will remain FD + 3/2 DG + GH equal to FB + 3/2 BA.

Deducting from one side GH, and from the other side 3/2 of AS, which are equal, there will remain FD with 3/2 DG equal to FB with 3/2 of BS.

But 3/2 of DG are equal to 3/2 of ES; then FD is equal to FB with 3/2 of BE. But DC was equal to 3/2 of EB; then deducting these equal lengths from one side and from the other, there will remain CF equal to FB. And thus it appears that the wave, the semi-diameter of which is DC, touches the arc BP at the moment when the light coming from the point L has arrived at B along the line LB.

It can be demonstrated similarly that at this same moment the light that has come along any other ray, such as LM, MN, will have propagated the movement which is terminated at the arc BP.

Whence it follows, as has been often said, that the propagation of the wave AH, after it has passed through the thickness of the glass, will be the spherical wave BP, all the pieces of which ought to advance along straight lines, which are the rays of light, to the centre F. Which was to be proved.

Similarly, these curved lines can be found in all the cases which can be proposed, as will be sufficiently shown by one or two examples which I will add.

Let there be given the surface of the glass AK, made by the revolution about the axis BA of the line AK, which may be straight or curved.

Let there be also given in the axis the point L and the thickness BA of the glass; and let it be required to find the other surface KDB, which receiving rays that are parallel to AB will direct them in such wise that after being again refracted at the given surface AK they will all be reassembled at the point L.

From the point L let there be drawn to some point of the given line AK the straight line LG, which, being considered as a ray of light, its refraction GD will then be found.

This line being then prolonged at one side or the other will meet the straight line BL, as here at V. Let there then be erected on AB the perpendicular BC, which will represent a wave of light coming from the infinitely distant point F, since we have supposed the rays to be parallel.

Then all the parts of this wave BC must arrive at the same time at the point L; or rather all the parts of a wave emanating from the point L must arrive at the same time at the straight line BC.

For that, it is necessary to find in the line VGD the point D such that having drawn DC parallel to AB, the sum of CD, plus 3/2 of DG, plus GL may be equal to 3/2 of AB, plus AL.

Or rather, on deducting from both sides GL, which is given, CD plus 3/2 of DG must be equal to a given length; which is a still easier problem than the preceding construction.

The point D thus found will be one of those through which the curve ought to pass; and the proof will be the same as before. And by this it will be proved that the waves which come from the point L, after having passed through the glass KAKB, will take the form of straight lines, as BC; which is the same thing as saying that the rays will become parallel.

Whence it follows reciprocally that parallel rays falling on the surface KDB will be reassembled at the point L.

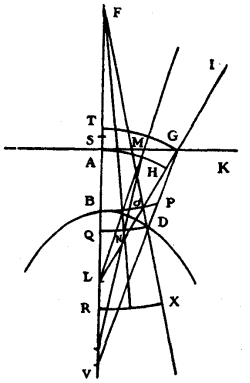
Let

• surface AK, of any desired form, generated by revolution about the axis AB
• the thickness of the glass at the middle be AB.
• the point L be given in the axis behind the glass; and let it be supposed that the rays which fall on the surface AK tend to this point, and that it is required to find the surface BD, which on their emergence from the glass turns them as if they came from the point F in front of the glass.

Having taken any point G in the line AK, and drawing the straight line IGL, its part GI will represent one of the incident rays, the refraction of which, GV, will then be found: and it is in this line that we must find the point D, one of those through which the curve DG ought to pass.

Let us suppose that it has been found: and about L as centre let there be described GT, the arc of a circle cutting the straight line AB at T, in case the distance LG is greater than LA; for otherwise the arc AH must be described about the same centre, cutting the straight line LG at H. This arc GT (or AH, in the other case) will represent an incident wave of light, the rays of which tend towards L.

Similarly, about the centre F let there be described the circular arc DQ, which will represent a wave emanating from the point F.

Then the wave TG, after having passed through the glass, must form the wave QD; and for this I observe that the time taken by the light along GD in the glass must be equal to that taken along the three, TA, AB, and BQ, of which AB alone is within the glass.

Or rather, having taken AS equal to 2/3 of AT, I observe that 3/2 of GD ought to be equal to 3/2 of SB, plus BQ; and, deducting both of them from FD or FQ, that FD less 3/2 of GD ought to be equal to FB less 3/2 of SB. And this last difference is a given length.

All that is required is to draw the straight line FD from the given point F to meet VG so that it may be thus. Which is a problem quite similar to that which served for the first of these constructions, where FD plus 3/2 of GD had to be equal to a given length.

In the demonstration it is to be observed that, since the arc BC falls within the glass, there must be conceived an arc RX, concentric with it and on the other side of QD. Then after it shall have been shown that the piece G of the wave GT arrives at D at the same time that the piece T arrives at Q, which is easily deduced from the construction, it will be evident as a consequence that the partial wave generated at the point D will touch the arc RX at the moment when the piece Q shall have come to R, and that thus this arc will at the same moment be the termination of the movement that comes from the wave TG; whence all the rest may be concluded.

Having shown the method of finding these curved lines which serve for the perfect concurrence of the rays, [Pg 123]there remains to be explained a notable thing touching the uncoordinated refraction of spherical, plane, and other surfaces: an effect which if ignored might cause some doubt concerning what we have several times said, that rays of light are straight lines which intersect at right angles the waves which travel along them.

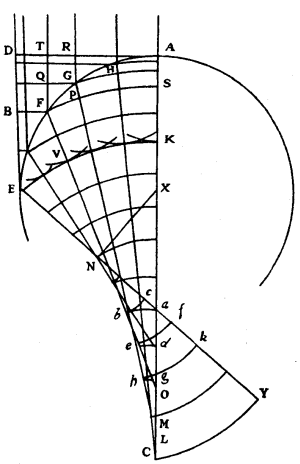
For example, in the case of rays which fall parallel on a spherical surface AFE, intersecting one another, after refraction, at different points, as this figure represents;

What can the waves of light be, in this transparent body, which are cut at right angles by the converging rays? For they can not be spherical.

What will these waves become after the said rays begin to intersect one another?

It will be seen in the solution of this difficulty that something very remarkable comes to pass herein, and that the waves do not cease to persist though they do not continue entire, as when they cross the glasses designed according to the construction we have seen.

According to what has been shown above, the straight line AD, which has been drawn at the summit of the sphere, at right angles to the axis parallel to which the rays come, represents the wave of light;

In the time taken by its piece D to reach the spherical surface AGE at E, its other parts will have met the same surface at F, G, H, etc. and will have also formed spherical partial waves of which these points are the centres.

The surface EK which all those waves will touch, will be the continuation of the wave AD in the sphere at the moment when the piece D has reached E. Now the line EK is not an arc of a circle, but is a curved line formed as the evolute of another curve ENC, which touches all the rays HL, GM, FO, etc., that are the refractions of the parallel rays, if we imagine laid over the convexity ENC a thread which in unwinding describes at its end E the said curve EK. For, supposing that this curve has been thus described, we will show that the said waves formed from the centres F, G, H, etc., will all touch it.

It is certain that the curve EK and all the others described by the evolution of the curve ENC, with different lengths of thread, will cut all the rays HL, GM, FO, etc., at right angles, and in such wise that the parts of them intercepted between two such curves will all be equal; for this follows from what has been demonstrated in our treatise de Motu Pendulorum.

Imagining the incident rays as being infinitely near to one another, if we consider two of them, as RG, TF, and draw GQ perpendicular to RG, and if we suppose the curve FS which intersects GM at P to have been described by evolution from the curve NC, beginning at F, as far as which the thread is supposed to extend, we may assume the small piece FP as a straight line perpendicular to the ray GM, and similarly the arc GF as a straight line.

But GM being the refraction of the ray RG, and FP being perpendicular to it, QF must be to GP as 3 to 2, that is to say in the proportion of the refraction; as was shown above in explaining the discovery of Des Cartes. And the same thing occurs in all the small arcs GH, HA, etc., namely that in the quadrilaterals which enclose them the side parallel to the axis is to the opposite side as 3 to 2.

Then also as 3 to 2 will the sum of the one set be to the sum of the other; that is to say, TF to AS, and DE to AK, and BE to SK or DV, supposing V to be the intersection of the curve EK and the ray FO.

But, making FB perpendicular to DE, the ratio of 3 to 2 is also that of BE to the semi-diameter of the spherical wave which emanated from the point F while the light outside the transparent body traversed the space BE.

Then it appears that this wave will intersect the ray FM at the same point V where it is intersected at right angles by the curve EK, and consequently that the wave will touch this curve.

In the same way it can be proved that the same will apply to all the other waves above mentioned, originating at the points G, H, etc. to wit, that they will touch the curve EK at the moment when the piece D of the wave ED shall have reached E.

Now to say what these waves become after the rays have begun to cross one another: it is that from thence they fold back and are composed of two contiguous parts, one being a curve formed as evolute of the curve ENC in one sense, and the other as evolute of the same curve in the opposite sense.

Thus the wave KE, while advancing toward the meeting place becomes abc, whereof the part ab is made by the evolute bC, a portion of the curve ENC, while the end C remains attached; and the part bc by the evolute of the portion bE while the end E remains attached.

Consequently the same wave becomes def, then ghk, and finally CY, from whence it subsequently spreads without any fold, but always along curved lines which are evolutes of the curve ENC, increased by some straight line at the end C.

There is even, in this curve, a part EN which is straight, N being the point where the perpendicular from the centre X of the sphere falls upon the refraction of the ray DE, which I now suppose to touch the sphere. The folding of the waves of light begins from the point N up to the end of the curve C, which point is formed by taking AC to CX in the proportion of the refraction, as here 3 to 2.

As many other points as may be desired in the curve NC are found by a Theorem which Mr. Barrow has demonstrated in section 12 of his Lectiones Opticae, though for another purpose. And it is to be noted that a straight line equal in length to this curve can be given.

For since it together with the line NE is equal to the line CK, which is known, since DE is to AK in the proportion of the refraction, it appears that by deducting EN from CK the remainder will be equal to the curve NC.

Similarly the waves that are folded back in reflexion by a concave spherical mirror can be found. Let ABC be the section, through the axis, of a hollow hemisphere, the centre of which is D, its axis being DB, parallel to which I suppose the rays of light to come.

All the reflexions of those rays which fall upon the quarter-circle AB will touch a curved line AFE, of which line the end E is at the focus of the hemisphere, that is to say, at the point which divides the semi-diameter BD into two equal parts.

The points through which this curve ought to pass are found by taking, beyond A, some arc AO, and making the arc OP double the length of it; then dividing the chord OP at F in such wise that the part FP is three times the part FO; for then F is one of the required points.

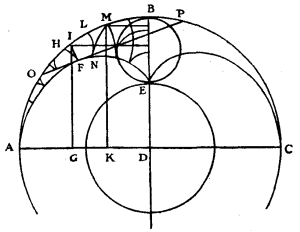
The parallel rays are merely perpendiculars to the waves which fall on the concave surface, which waves are parallel to AD, it will be found that as they come successively to encounter the surface AB, they form on reflexion folded waves composed of two curves which originate from two opposite evolutions of the parts of the curve AFE.

So, taking AD as an incident wave, when the part AG shall have met the surface AI, that is to say when the piece G shall have reached I, it will be the curves HF, FI, generated as evolutes of the curves FA, FE, both beginning at F, which together constitute the propagation of the part AG.

A little afterwards, when the part AK has met the surface AM, the piece K having come to M, then the curves LN, NM, will together constitute the propagation of that part. And thus this folded wave will continue to advance until the point N has reached the focus E.

The curve AFE can be seen in smoke, or in flying dust, when a concave mirror is held opposite the sun. It should be known that it is none other than that curve which is described by the point E on the circumference of the circle EB, when that circle is made to roll within another whose semi-diameter is ED and whose centre is D.

So that it is a kind of Cycloid, of which, however, the points can be found geometrically.

Its length is exactly equal to 3/4 of the diameter of the sphere, as can be found and demonstrated by means of these waves, nearly in the same way as the mensuration of the preceding curve; though it may also be demonstrated in other ways, which I omit as outside the subject.

The area AOBEFA, comprised between the arc of the quarter-circle, the straight line BE, and the curve EFA, is equal to the fourth part of the quadrant DAB.

END