Incommensurable magnitudes

Proposition 2

If the remainder of 2 unequal magnitudes (which are) [laid out] never measures the (magnitude) before it, (when) the lesser (magnitude is) continually subtracted in turn from the greater, then the (original) magnitudes will be incommensurable.

For, AB and CD being two unequal magnitudes, and AB (being) the lesser, let the remainder never measure the (magnitude) before it, (when) the lesser (magnitude is) continually subtracted in turn from the greater. I say that the magnitudes AB and CD are incommensurable.

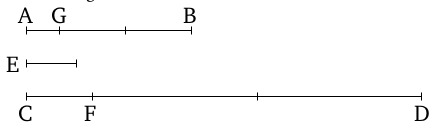
For if they are commensurable then some magnitude will measure them (both). If possible, let it (so) measure (them), and let it be E.

Let AB leave CF less than itself (in) measuring FD, and let CF leave AG less than itself (in) measuring BG, and let this happen continually, until some magnitude which is less than E is left.

Let (this) have occurred, and let AG, (which is) less than E, have been left. Therefore, since E measures AB, but AB measures DF, E will thus also measure FD. And it also measures the whole (of) CD.

Thus, it will also mea- sure the remainder CF. But, CF measures BG. Thus, E also measures BG. And it also measures the whole (of) AB. Thus, it will also measure the remainder AG, the greater (measuring) the lesser.

The very thing is impos- sible. Thus, some magnitude cannot measure (both) the magnitudes AB and CD. Thus, the magnitudes AB and CD are incommensurable [Def. 10.1).

Thus, if… of two unequal magnitudes, and so on….

Proposition 3

Find the greatest common measure of two given commensurable magnitudes.

AF H G H CE B Let AB and CD be the two given magnitudes, of which (let) AB (be) the lesser. So, it is required to find the greatest common measure of AB and CD. For the magnitude AB either measures, or (does) not (measure), CD. Therefore, if it measures (CD), and (since) it also measures itself, AB is thus a common mea- sure of AB and CD. And (it is) clear that (it is) also (the) greatest. For a (magnitude) greater than magnitude AB cannot measure AB. So let AB not measure CD. And continually subtract- ing in turn the lesser (magnitude) from the greater, the remaining (magnitude) will (at) some time measure the (magnitude) before it, on account of AB and CD not be- ing incommensurable [Prop. 10.2]. And let AB leave EC less than itself (in) measuring ED, and let EC leave AF less than itself (in) measuring FB, and let AF measure CE.

Therefore, since AF measures CE, but CE measures FB, AF will thus also measure FB. And it also mea- sures itself. Thus, AF will also measure the whole (of) AB. But, AB measures DE. Thus, AF will also mea- sure ED. And it also measures CE. Thus, it also mea- sures the whole of CD. Thus, AF is a common measure of AB and CD. So I say that (it is) also (the) greatest (common measure). For, if not, there will be some mag- nitude, greater than AF, which will measure (both) AB and CD. Let it be G. Therefore, since G measures AB, but AB measures ED, G will thus also measure ED. And it also measures the whole of CD. Thus, G will also mea- sure the remainder CE. But CE measures FB. Thus, G will also measure FB. And it also measures the whole (of) AB. And (so) it will measure the remainder AF, the greater (measuring) the lesser. The very thing is im- possible. Thus, some magnitude greater than AF cannot measure (both) AB and CD. Thus, AF is the greatest common measure of AB and CD. Thus, the greatest common measure of two given commensurable magnitudes, AB and CD, has been found. (Which is) the very thing it was required to show. Corollary So (it is) clear, from this, that if a magnitude measures two magnitudes then it will also measure their greatest common measure.

Proposition 4

To find the greatest common measure of three given commensurable magnitudes.

A B C DE F Let A, B, C be the three given commensurable mag- nitudes. So it is required to find the greatest common measure of A, B, C. For let the greatest common measure of the two (mag- nitudes) A and B have been taken [Prop. 10.3], and let it be D. So D either measures, or [does] not [measure], C. Let it, first of all, measure (C). Therefore, since D mea- sures C, and it also measures A and B, D thus measures A, B, C. Thus, D is a common measure of A, B, C. And (it is) clear that (it is) also (the) greatest (common mea- sure). For no magnitude larger than D measures (both) A and B. So let D not measure C. I say, first, that C and D are commensurable. For if A, B, C are commensurable then some magnitude will measure them which will clearly also measure A and B. Hence, it will also measure D, the greatest common measure of A and B [Prop. 10.3 corr.]. And it also measures C. Hence, the aforementioned mag- nitude will measure (both) C and D. Thus, C and D are commensurable [Def. 10.1]. Therefore, let their greatest common measure have been taken [Prop. 10.3], and let it be E. Therefore, since E measures D, but D measures (both) A and B, E will thus also measure A and B. And it also measures C. Thus, E measures A, B, C. Thus, E is a common measure of A, B, C. So I say that (it is) also (the) greatest (common measure). For, if possible, let F be some magnitude greater than E, and let it measure A, B, C. And since F measures A, B, C, it will thus also measure A and B, and will (thus) measure the greatest common measure of A and B [Prop. 10.3 corr.]. And D is the greatest common measure of A and B. Thus, F measures D. And it also measures C. Thus, F measures (both) C and D. Thus, F will also measure the greatest common measure of C and D [Prop. 10.3 corr.]. And it is E. Thus, F will measure E, the greater (measuring) the lesser. The very thing is impossible. Thus, some [magni- tude] greater than the magnitude E cannot measure A, B, C. Thus, if D does not measure C then E is the great- est common measure of A, B, C. And if it does measure (C) then D itself (is the greatest common measure). Thus, the greatest common measure of three given commensurable magnitudes has been found. [(Which is) the very thing it was required to show.] Corollary So (it is) clear, from this, that if a magnitude measures three magnitudes then it will also measure their greatest common measure. So, similarly, the greatest common measure of more (magnitudes) can also be taken, and the (above) corol- lary will go forward. (Which is) the very thing it was required to show.