Gaussian Co–ordinates

The solution of Gauss is as follows.

We draw arbitrary u-curves u = 1 , u = 2 and u = 3 on the surface of the marble slab. Between u = 1 and u = 2 are an infinitely large number of curves corresponding to real numbers between 1 and 2.

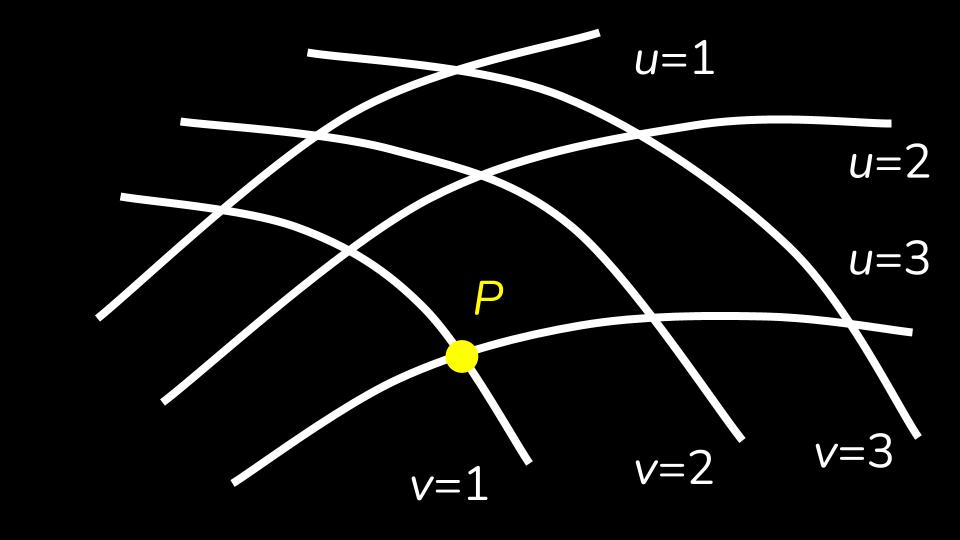
These u-curves must not intersect each other. Through each point of the surface one and only one curve must pass. Thus, a definite value of u belongs to every point on the surface of the marble slab.

Next, we draw v-curves on the surface, similar to the u curves. These have numbers and have an arbitrary shape. It follows that a value of u and v belong to every point on the surface. We call these two numbers the Gaussian coordinates.

For example:

• the point P in the diagram has the Gaussian coordinates u = 3 , v = 1.
• 2 neighbouring points P and P' have the co-ordinates where du and dv signify very small numbers:

P  =  u, v
P' =  u + du, v + dv,

The distance (line-interval) between P and P', measured with a little rod, is shown through the very small number ds. Thus, we have:

ds^2 = g11 du^2 + 2g12 du dv + g22 dv^2

where g11, g12, g22 are magnitudes which depend in a definite way on u and v. The magnitudes g11, g12, and g22 determine the behaviour of the rods relative to the u-curves and v-curves, and thus also relative to the surface of the table.

2D Euclidean Continuum

In certain conditions, the points form a Euclidean continuum with reference to the measuring-rods. In this case, it is possible to draw the u-curves and v-curves and attach numbers to them:

ds^2 = du^2 + dv^2 .

Under these conditions, the u-curves and v-curves are:

• Euclidean straight lines
• perpendicular to each other

Here, the Gaussian co-ordinates are simply Cartesian ones.

• They are merely an association of 2 sets of numbers with the points of the surface. These numbers differ very slightly from each other and are associated with neighbouring points “in space.”

So far, these considerations hold for a continuum of 2D.

3D Gaussian Continuum

The Gaussian method can also be applied to a continuum of 3 or more dimensions. A 4D continuum is reprsented by the following.*

Each point of the continuum has 4 arbitrary numbers x1 , x2 , x3 , x4 as “co-ordinates.” Adjacent points correspond to adjacent values of the co-ordinates.

A distance ds is associated with the adjacent points P and P'. This distance is measurable and well-defined from a physical point of view. This leads to the formula:

ds^2 = g11 dx1^2 + 2g12 dx1 dx2 . . . . + g44 dx4^2

where the magnitudes g11, etc, have values which vary with the position in the continuum.

Only when the continuum is a Euclidean one is it possible to associate the co-ordinates x1 . . x4 with the points of the continuum so that we have simply:

ds^2 = dx1^2 + dx2^2 + dx3^2 + dx4^2

In this case, relations hold in the 4D continuum which are analogous to those holding in our 3D measurements.

However, the Gauss treatment for ds^2 which we have given above is not always possible. It is only possible when sufficiently small regions of the continuum under consideration may be regarded as Euclidean continua.

An example is when the marble slab is heated from the center. The temperature is constant for a small part of the slab [on the sides]*. Thus, the geometrical behaviour of the rods follows the rules of Euclidean geometry.

Hence, the imperfection of the squares in Section 24 are not evident until this construction is extended over a considerable portion of the table’s surface.

Gauss invented a method for the mathematical treatment of continua in general, wherein “size-relations” are defined. These “size-relations” are “distances” between neighbouring points.

• Each point in a continuum has an assigned number.
• The numbers are as many as the continuum has dimensions.
• Each assignment has only one meaning.
• The numbers, as Gaussian co-ordinates, which differ by an indefinitely small amount are assigned to adjacent points.

The Gaussian co-ordinate system is a logical generalisation of the Cartesian co-ordinate system.

It is also applicable to non-Euclidean continua only when the small parts (in terms of size or distance) of the continuum behave more nearly like a Euclidean system, emphasizing the smaller the part of the continuum.