A Few Inferences From General Relativity

Section 20 showed that General Relativity (GR) lets us derive properties of the gravitational field in a purely theoretical way*.

*Superphysics Note: Yes, it’s only theoretical just as Genesis is theoretical and not real!

Let us suppose that we know the space-time “course” for any path in Galileian space relative to a non-moving viewpont.

Through theoretical calculation, we can find how this path appears, as seen from a moving viewpoint `K'` which is moving relatively to `K`. But since this new viewpoint `K'` has its own gravitational field, we can find out how such a field influences the parth.

For example, a body moving straight with respect to K (according to the law of Galilei) is executing an accelerated and curvilinear motion with respect to the moving glass box K' in Section 20 . Its acceleration or curvature is affected by the gravitational field in K'.

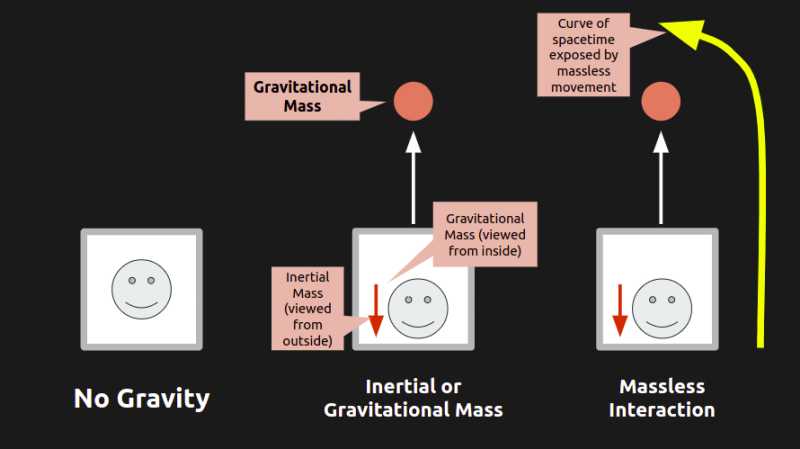
However, we get a different result when we replace that body with a ray of light.

• It travels in a straight line with the velocity c relative to the moving glass box.
• But its path will be in a curve when seen from the relative to moving glass box.

This means that generally, light curves in gravitational fields.

This is very important because:

1. This happens in reality.

The curvature of light rays by gravity is very small. Nevertheless, the curve for light rays passing the sun at grazing incidence is 1.7 seconds of arc.

From the earth’s viewpoint, certain fixed stars are seen around the sun during a total eclipse. These stars should then appear displaced away from the sun by 1.7 seconds of arc compared to their apparent position in the sky when the sun is elsewhere*.

*Einstein Note: Through star photographs, the Joint Committee of the Royal and Royal Astronomical Societies confirmed the deflection of light demanded by GR during the solar eclipse of 29th May, 1919.

2. The constant speed of light in vacuum cannot be totally valid, according to GR.

Since light rays can only curve when light changes position, one might think that this invalidates Special Relativity (SR), and with it the whole theory of relativity. But this is not the case.

It just means that Special Relativity is not valid universally. Special Relativity only holds if we disregard the influence of gravitational fields on light. Opponents of Relativity say that Special Relativity is overthrown by the General Relativity. But they are wrong.

Before the development of electrodynamics, the laws of electrostatics and the laws of electricity were regarded indiscriminately. Nowadays, we know that electric fields can be derived correctly from electrostatic considerations only when the electrical masses are at rest relative to each other. But we do not overthrow electrostatics because of Maxwell’s field-equations.

Electrostatics is contained in electrodynamics as a limiting case.

The laws of electrodynamics lead directly to laws of electrostatics when the fields are invariable with regard to time*.

Superphysics Note: Here Einstein shows his sophistry. Electrostatics is a part of Electrodynamics just as a car being able to part (have a handbrake) is a part of the whole design for a moving car. But General Relativity is different because it is a sophistical extension of Maxwell-Lorentz onto outerspace and gravity. It is like adding wings to a car to make it into a flying car yet applying road rules in flight.

Special Relativity points to a more comprehensive theory in the form of General Relativity.

Through the bending of light by gravity, General Relativity enables us to theoretically derive the influence of a gravitational field on light (The laws of light we already know when gravity is absent.)

General Relativity solves* the gravitational field itself.

*Superphysics Note: No, it doesn’t. It actually makes gravity more confusing because it is totally different from Newton who clearly saw gravity as a force.

We already know what happens to spacetime without gravity. A gravity-less moving body K' will interact with a gravitational field which is variable with respect to space and time*. The character of this field will depend on K'’s motion.

*Einstein note: This follows from a generalisation of Section 20.

According to GR, the general law of the gravitational field applies. Not all gravitational fields are produced in this way [exposed by moving bodies].

Yet we can hope that such kinds of gravitation will lead to a general law of gravitation*.

*Superphysics Note: After 100 years, no general law of gravitation has been derived from GR because his gravitation was a sophistry in the first place.