The Relativity Of Simultaneity

A very long train travels with the constant velocity v.

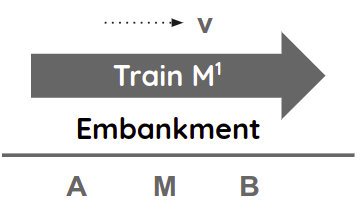
People in this train will use the train as a rigid viewpoint for all events relative to the train.

Lightning strikes A and B simultaneously from the viewpoint of the embankment. Is it also simultaneous from the viewpoint of the train?

It is not.

The light arriving at A and B meet each other at the mid-point M of the embankment. But the events A and B also correspond to positions A and B on the train.

M' is the mid-point of the train. When the lightning strikes, M' naturally coincides with the M. But it moves forwards according to the train’s velocity v.

If an observer in the train at M' sat still and the train was also still, then the light from the lightning at A and B would reach him simultaneously. But if the train were traveling forward and he is walking forward to B, then he will see the beam of light emitted from B earlier than that from A. Thus, observers in the train will think that lightning flash B happened earlier than lightning flash A.

Thus:

• events which are simultaneous with reference to the embankment are not simultaneous with respect to the train, and vice versa (relativity of simultaneity).
• every reference-body or viewpoint has its own time.
• an event’s time has no meaning if we do not know which viewpoint that event’s time takes

Before my theory of relativity, physicists assumed that time had an absolute significance*, i.e. that it is independent of the motion of the body of reference.

*Superphysics Note: Time has an absolute significance to the Material layer, semi-significance to the Electromagnetic layer, and no significance (or very tiny significance) to the aetheral layer (e.g. time flies fast when you’re having fun). Einstein is therefore employing sophistry by applying the principle of the Electromagnetic layer to all layers.

But this assumption is incompatible with the most natural definition of simultaneity. If we discard this assumption, then the conflict between the law of the propagation of light in a vacuum and the principle of relativity (in Section 7) disappears.

But this leads us to conflict with Section 6 [the adding of velocities]. This is because the man in the train is moving forward at a distance w per second with the train. But, according to this section, the time of an event in the train from the train’s viewpoint is not equal to the timespan of the same event viewed from the embankment (as reference-body).

Hence, from the viewpoint of the embankment, the walking man does not travel at the same speed as when viewed from inside the train.