The System Of Co–ordinates

by Albert Einstein Icon

4 minutes • 705 words

Table of contents

Standard Measuring Rod

Standard Measuring Rod

To measure the distance between two points on a rigid body, we need a measuring rod as Rod S as a standard measure.

Assuming there is Point A and B are on a rigid body. We can draw a line joining them starting from Point A. We can mark off the distance S time after* time until we reach B. The number of these operations required is the numerical measure of the distance AB.

*Superphysics note: This is similar to Newton drawing mini-rectangles to draw curves in Calculus. We shall call this the Calculus way

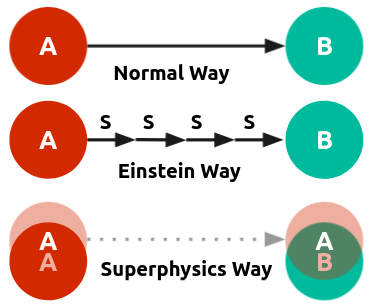
Einstein's movement — Einstein’s innovation was to chop up a single perception into smaller ones, which eventually became quanta. Superphysics views all movement as being sourced internally and so the the movement is actually a change in location from a change in internal volition from Volition A into Volition B. For non-living identities, we replace ‘volition’ with ‘gravitational signature

This is the basis of all measurement of length*.

*Einstein footnote: The measurement is always in a whole number because we use divided measuring-rods

All events or positions of objects in space are based on points on a rigid body (body of reference) where those events or objects exist.

For example, “Trafalgar Square, London” is a point on the rigid body called the earth

This primitive method of place specification=

deals only with places on the surface of rigid bodies, and
is dependent on distinguishable points on this surface

But we can free ourselves from both of these limitations without altering the nature of our specification of position.

If, for instance, a cloud is hovering over Trafalgar Square, then we can determine its position relative to the surface of the earth by erecting a pole perpendicularly on the Square, so that it reaches the cloud.

The pole’s length measured with the standard measuring-rod, combined with the location of the pole’s base, gives us a complete measurement.

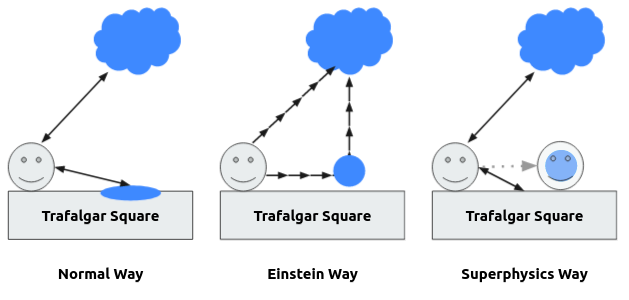
This gives us a better way to view position:

We imagine the rigid body, to which the place specification is referred, supplemented in such a manner that the object whose position we require is reached by the completed rigid body.
In locating the position of the object, we make use of a number (here the length of the pole measured with the measuring-rod) instead of designated points of reference.
We speak of the height of the cloud even when the pole which reaches the cloud has not been erected.

We can determine the length of the pole needed to reach the cloud by=

seeing the cloud from different positions on the ground, and
taking into account the properties of light

This will allow us to describe positions mathematically without needing fixed, marked positions on the rigid body of reference.

For this, we can use the Cartesian system of co-ordinates which are made of three plane surfaces perpendicular to each other and rigidly attached to a rigid body.

The position of any event will be determined by specifying the lengths of the three perpendiculars or co-ordinates (x, y, z) which can be dropped from the scene of the event to those three plane surfaces.

The lengths of these three perpendiculars can be determined by a series of manipulations with rigid measuring-rods performed according to the rules of Euclidean geometry.

If the results of physics and astronomy are to maintain their clearness, the physical meaning of specifications of position must always be sought in accordance with the above considerations. 1 We thus obtain the following result=

Thus, all events in space involves the use of a rigid body where those events happen. The relationship between events, as ‘distances’, follow Euclidean geometry represented by marks on the rigid body.