The 7 Rules That Determining Motion After Collision

45. The rules for determining how much the motion of each body is changed because of the collision of other bodies

Collisions with other bodies cause bodies to:

• increase or decrease their motions, or
• turn elsewhere

In order to calculate such changes, we only need to:

• subtract the amount of force in each, either to move or to resist motion, and
• establish for certain that which is stronger always achieves its effect.

This could easily be deduced by calculation if:

• only 2 bodies encountered each other mutually
• they were perfectly hard, and separated from all others.
  • In this way, their motions were not impeded by any other surrounding bodies, nor assisted.

They then would follow the following rules.

46. Rule 1

Assume Body B and C, were perfectly equal and moving at equal speeds. B is moving from right to left, and C from left to right.

When they encountered each other, they would be reflected and then continue to move, B to the right, and C to the left, without any loss of their speed.

47. Rule 2

If B were just slightly larger than C, then only C would be reflected. Both would move to the left with the same speed.

48. Rule 3

If they were equal in mass, but B moved slightly faster than C, they would both continue moving to the left. Some of B’s excess speed would be transferred to C.

If:

• B had 6 units of speed
• C had 4 units

After the collision, each would move to the left with 5 units of speed.

49. Rule 4

Assume body C were completely at rest and slightly larger than B. No matter how fast B moved towards C, it would never move C.

Instead, it would be repelled by C in the opposite direction.

This is because a stationary body resists high velocity more than low velocity, in proportion to the excess of one over the other.

Therefore, the force in C to resist would always be greater than in B to propel.

50. Rule 5

Assume that body C were stationary and smaller than B.

No matter how slowly B moved towards C, it would move C with it, transferring a portion of its own motion to it, so that both would subsequently move at the same speed.

Specifically, if B were twice as large as C, it would transfer to C 1/3 of its motion.

This is because that 1/3 would move the body C as quickly as the remaining 2/3 would move the body B, which is twice as large.

So, after B had encountered C, it would move 1/3 slower than before. It would take the same amount of time to move through a space of 2 feet as it did before to move through a space of 3 feet.

Similarly, if B were 3 times larger than C, it would transfer to C 1/4 of its motion, and so on for the rest.

51. Rule 6

If the mass of stationary body C were precisely equal to that of the moving body B, when B approached C with 4 units of speed, it would:

• transfer 1 unit of speed to C
• be reflected with the remaining 3 units in the opposite direction.

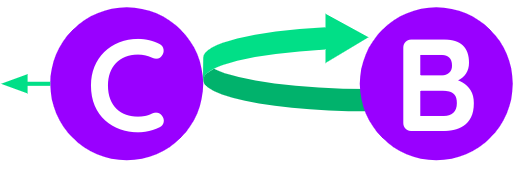
52. Rule 7

Assume B and C were moving towards the same direction.

• C was moving slower, with B eventually catching up to it
• C were larger than B
• The speed of B was greater than the excess of size in C

Then B would transfer just enough of its motion to C so that both would subsequently move at the same speed and direction.

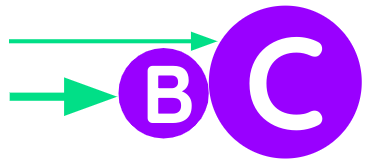
However, if the excess of speed in B were less than the excess of size in C, then B would be reflected in the opposite direction and retain all of its motion.

These excesses are calculated as follows:

• If C were twice as large as B and B did not move twice as fast as C, it would not propel C but would be reflected in the opposite direction.
• If it moved more than twice as fast, it would propel C.

For instance, if C had only 2 units of speed and B had 5, subtracting 2 units from B would transfer only 1 unit to C.

This would make both bodies move with 3 units of speed thereafter. This is because C is twice as large as B.

This would result in both bodies, B and C, moving with 3 units of speed.

This reasoning applies similarly to other cases.