Relationality: Math Versus Supermath
Table of Contents
For example, a basic math equation is 1 + 1 = 2. This can be visualized by:

Notice how this is overly simplistic and does not expand on cause and effect. This is because math uses a constricted mindset that really relies on the Conservation of Ideas.
This is why math-people can flip or transpose things. For example, 1 + 1 = 2 can be transposed to 2 = 1 + 1. This is because the = sign “conserves` the values on both sides.
The problem is that this is for closed, finite things and does not work for things that cross over to the aethereal layer. For example, the mass of a subatomic particle might be:
1 + 1 = 2.0000123
Math will be unable to explain where the .0000123 came from, which Superphysics explains could come from the upper layers or by abnormal properties of the particle in certain situations.
To fix this, we turn 1 + 1 = 2 into qualimath by adding the necessary parts:
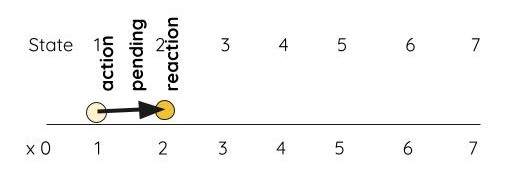
Here, we expose that the focus of the equation or line is itself. The qualimath ratio is State 1 :: State 2 which we deconstruct as:
(1 + 1) :: 2
This leads to the same output as the 1 + 1 = 2 of normal math, while imposing the following mental changes:
1 + 1is a rigid ratio of2, not an equality. It means it is confined to specific layer and does not cross over to other layers. This is useful when it comes to constants
- Both sides have the same importance
- A straight-line equation would imply that the focus or dharma is on the line itself. A curved or wavy line would have its dharma harder to expose.
- A straight-line equation is like a person who goes to McDonalds to order a cheeseburger specifically
- A curve equation is like a person who orders a cheeseburger then changes his order to a chicken meal then changes to a chicken burger as a compromise between his 2 previous orders. His dharma is neither burger nor chicken, but chicken burger
The Ratio and Rigid Ratio
The ratio signs are derived from programming which uses =, ==, and ===
=is assignment. This is similar to our:==is loose equality. This is similar to our::===is strict equality. This is similar to our=
The concept of a focus is super important as it is the basis of:
- gravitational signatures
- the hierarchy of the universe
- Descartes’ First and Third Rules of Motion
But for 1 + 1 = 2.0000123, we use a different ratio:
(1 + 1) : 2.0000123
This means that the inequality is caused by something unknown. Provisionally, we fix this with:
(1 + 1) : 0.0000123 aether :: 2.0000123
The 0.0000123 aether is a value from the aethereal layer that is affecting the relationship.
A More Complex Example
Let’s say we want to convert 17 * 19 = 323 to Qualimath. This will create 3 states in our sandbox:
- State 1 for
17 - Pseudo-state or action for
19 - State 2 for the
answer
We notate this as (State 1 * action) :: State 2, deconstructed as (17 * 19) :: answer
We use Egyptian Math, as Al-Khwarizmis algorithms, to deconstruct 17 (State 1) into its doubles as a ratio of the doubles of 19 (action).
| State 1: 17 | Action: 19 |
|---|---|
| 1 | 19 |
| 2 | 38 |
| 4 | 76 |
| 8 | 152 |
| 16 | 304 |
We use State 1 as the focus and add the corresponding values in the action* to get State 2 as 323**.
*Action is a pseudo state of State 1 that allowed the change. Without that pseudo-state, then State 1 would stay close minded and not be open to change and therefore remain as State 1 instead of changing to State 2.
*323 = 304 [as 5th row of State 2 or 16] + 19 [as 1st row of State 1 or 1 to get 17]
Here, the smaller number is put before the larger. In case of multiple multipliers, the first 2 are combined then rearranged, then multiplied with the latter multipliers.
This use of states, foci, and arrangements greatly simplifies math instead of making it boring and burdensome.
Modern algebra has so many certain rules and formulas that it is full of confusion and obscurity that embarrasses instead of cultivating the mind.
Rene Descartes
Method of Reasoning and seeking Truth in the Sciences Simplified, Part 2