Vortex Numbers and Fractals
Vortex numbers are base-5 instances that can make geometry easier and less irrational


Vortex Numbers
Section 1

Constants and Bases
Section 2
Popular Constants
Section 3
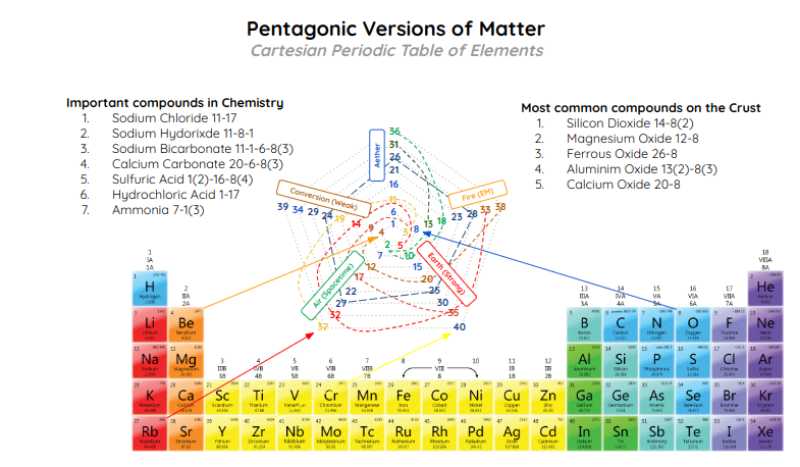
The Periodic Table of Elements as Qualitative Instances
Section 4

Fractals
Section 4