Problems that can be constructed using only circles and straight lines

Consider the lines AB, AD, AF, and similar ones traced with the instrument YZ.

The instrument is composed of several rulers joined together so that YZ is along line AN.

• This allows the angle XYZ to be opened and closed.

When this angle is fully closed, the points B, C, D, E, F, G, H are all assembled at point A.

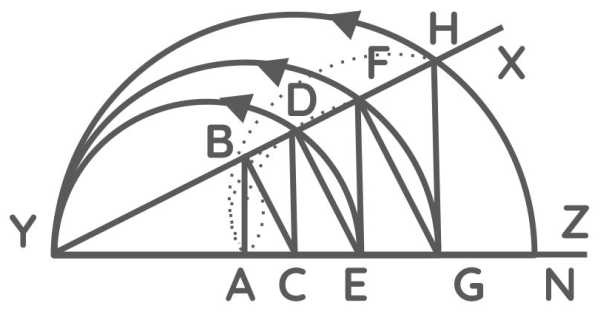
But as the angle is opened, the ruler BC, which is joined at a right angle to XY at point B, pushes the ruler CD along YZ, always forming right angles with it.

CD pushes DE, which also slides along YX, remaining parallel to BC

DE pushes EF EF pushes FG which in turn pushes GH, and so on

This leads to an infinite number of others pushing each other successively in the same way, some always making the same angles with YX and others with YZ.

As the angle XYZ is thus opened, point B draws the curve AB, which is a circle.

The other points D, F, H, where the other rulers intersect, draw other curves AD, AF, AH.

• Each these is more complex than the one before
• AB itself is more complex than the circle.

But I see nothing that should prevent us from conceiving the description of this first one as clearly and distinctly as that of the circle, or at least as clearly as the conic sections.

Nor do I see what should prevent us from conceiving the second, the third, and all the others that can be described, just as well as the first.

Consequently, they are all equally as valid for geometric investigation

How to distinguish all curved lines into certain types and understand the relationship of their points to those of straight lines

There are many other ways to draw and conceive curved lines that become increasingly complex by degrees to infinity.

but in order to understand all those that exist in nature collectively, and to distinguish them in an orderly manner into certain types, I know of nothing better than to say that all the

All geometric points are those which fall under some precise and exact measurement.

• These necessarily have some relationship to all the points of a straight line
• This line can be expressed by some equation, always by the same one

When this equation goes no higher than the rectangle (product) of 2 indeterminate quantities, or the square of one, the curved line is of the first and simplest kind.

• Within this, only the circle, the parabola, the hyperbola, and the ellipse are included

But when the equation rises to the third or fourth degree of either or both of the indeterminate quantities (for two are needed here to explain the relationship of one point to another), it is of the second kind

When the equation rises to the fifth or sixth degree, it is of the third kind; and so on to infinity.

The curve EC (fig. 8) goes from the intersection of the ruler GL and the plane CNKL.

• Its side KN is extended indefinitely toward C
• This makes its diameter KL always applied to some point on the line BA extended in both directions.
• This causes the ruler GL to move circularly around point G, since it is so joined to G that it always passes through point L.

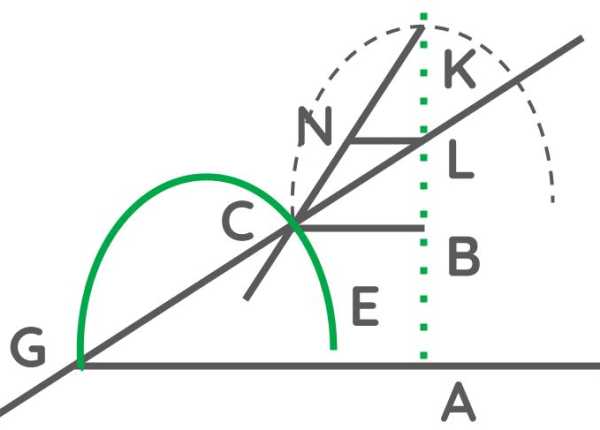
To determine what kind is curve EC, I choose a straight line like AB, to relate to its various points all those of the curved line EC.

• On this line AB, I begin my calculation at a point such as A

I choose both (the point and the line) because we are free to take them as we wish.

In whatever way we choose them, the curve will always be of the same type. Then choose a point arbitrarily on the curve, such as C.

I draw from C the line CB, parallel to GA.

CB and BA are 2 unknown and undetermined quantities, I name one y and the other x.

But in order to find the relationship between the two, I also consider the known quantities that determine the description of this curve, such as:

• GA, which I call a
• KL which I call b
• NL, parallel to GA, which I call c

As NL is to LK, or c to b, so is CB or y to BK, which is therefore (b/c)y.

BL is (b/c)y − b, and AL is x + (b/c)y − b.

Moreover, as CB is to LB, or y to (b/c)y − b, so is AG or a to LA, or x + (b/c)y − b. Thus, multiplying the second by the third gives:

(a·b/c)y − ab,

which is equal to

xy + (b/c)y² − by,

which is obtained by multiplying the first by the last.

And so, the equation that had to be found is:

y² = (cy − cx/b)y + ay − ac

From which we recognize that the curve EG is of the first type, as it is indeed nothing other than a hyperbola.

Instead of using line CNK, we make it a hyperbola or some other Type 1 curve that bounds the plane CNKL.

• Te intersection of this curve and the ruler GL will draw another curve of a second type, instead of the hyperbola EC

For example, if CNK is a circle with L as its center, one will describe the first conchoid of the ancients;

If it is a parabola with diameter KB, one will describe the curve I previously said is the first and simplest in Pappus’s problem, when only five straight lines are given by position.

But if, instead of one of these first-type curves, the bounding curve CNKL is of the second type, one will describe with it a curve of the third type.

If it is of the third type, then a curve of the fourth type, and so on to infinity, as is very easy to see by calculation.

In whatever way one imagines the construction of a curved line, as long as it is among those I call geometrical, one can always find an equation to determine all its points in this manner.

I classify curves as the following:

1. Those equations that rise only to the square in the same type as those that go up to the cube
2. Those equations that go to the square of a cube, in the same type as those that rise only to the biquadratic (fourth degree)
3. so on for the rest.

This is because there are general rules to:

• reduce to the cube all the problems that rise to the biquadratic,
• reduce to the biquadratic all those that rise to the square of a cube, so that they should not be considered more complex.